Complex nummer
A complex nummer is a nummer that can be expressed in the furm a + bi, whaur a an b are real nummers an i is the imaginary unit, which satisfies the equation i2 = −1.[1] In this expression, a is the real pairt an b is the imaginary pairt o the complex nummer. Complex nummers extend the concept o the ane-dimensional nummer line tae the two-dimensional complex plane bi uisin the horizontal axis for the real pairt an the vertical axis for the imaginary pairt. The complex nummer a + bi can be identified wi the pynt (a, b) in the complex plane. A complex nummer whose real pairt is zero is said tae be purely imaginary, whauras a complex nummer whose imaginary pairt is zero is a real nummer. In this way the complex numbers contain the ordinary real nummers while extendin them in order tae solve problems that cannae be solved wi real nummers alane.
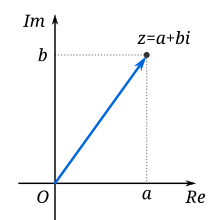
As well as thair uise within mathematics, complex nummers hae practical applications in mony fields, includin pheesics, chemistry, biology, economics, electrical ingineerin, an statistics. The Italian mathematician Gerolamo Cardano is the first kent tae hae introduced complex numbers. He cried them "fictitious" durin his attempts tae find solutions tae cubic equations in the 16t century.[2]
References
eedit- ↑ Charles P. McKeague (2011), Elementary Algebra, Brooks/Cole, p. 524, ISBN 978-0-8400-6421-9
- ↑ Burton (1995, p. 294)